若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）A.A与B相似 B. C.A=B D.A与B不一定相似，但|A|=|B|
题目
A.A与B相似
B.
C.A=B
D.A与B不一定相似，但|A|=|B|
相似考题
更多“若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ） ”相关问题
-
第1题：
设n阶矩阵A有一个特征值3，则|-3E+A|=_________.
正确答案：
0 -
第2题：
设A为n阶方阵，则A可对角化的充分必要条件是( ).
A. A有n个不同特征值
B.A有n个不同特征向量
C.A有n个线性元关的特征向量
D.IAI≠0。
参考答案：C
-
第3题：
任意n阶实称矩阵都存在n个线性无关的特征向量。()
参考答案：正确
-
第4题：
已知二阶实对称矩阵A的特征值是1，A的对应于特征值1的特征向量为（1，－1）T，若|A|＝－1，则A的另一个特征值及其对应的特征向量是（ ）。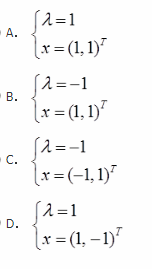
答案：B解析：根据矩阵行列式与特征值的关系：|A|＝λ1λ2，故另一个特征值为－1，其对应的特征向量应与已知特征向量正交，即两向量点乘等于零，因此（1，1）T满足要求。 -
第5题：
若A是m×n矩阵，且m≠n，则当A的列向量组线性无关时，A的行向量组也线性无关答案：错解析： -
第6题：
设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵
B.A有不为0的特征值
C.A的特征值全为0
D.A有n个线性无关的特征向量答案：C解析：
-
第7题：
若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为：
A. a B.-a
C. 0 D. a-1答案：A解析：解：本题主要考察两个知识点：特征值的求法及行列的运算。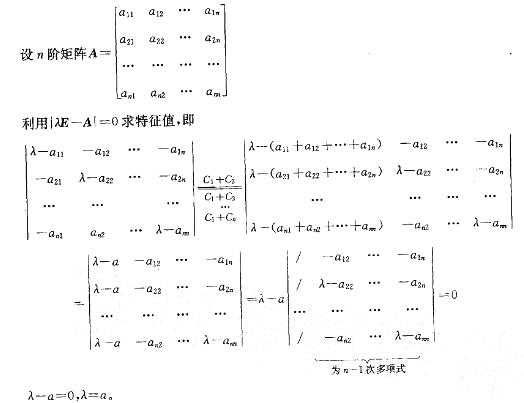
A的一特征值为a。
选A。 -
第8题：
设A是nxm矩阵，B是mxn矩阵，E是n阶单位阵，若AB=E，证明B的列向量组线性无关。答案：解析：
-
第9题：
设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明：λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量？说明理由.答案：解析：
-
第10题：
设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是( )。
A. α是矩阵-2A的属于特征值-2λ的特征向量
D. α是矩阵AT的属于特征值λ的特征向量答案：D解析：提示：显然A、B、C都是正确的。 -
第11题：
单选题设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。Aα是矩阵-2A的属于特征值-2λ的特征向量
Bα是矩阵的属于特征值的特征向量
Cα是矩阵A*的属于特征值的特征向量
Dα是矩阵AT的属于特征值λ的特征向量
正确答案： B解析： 暂无解析 -
第12题：
问答题设有三个非零的n阶（n≥3）方阵A1、A2、A3，满足Ai2＝Ai（i＝1，2，3），且AiAj＝0（i≠j，i、j＝1，2，3），证明： （1）Ai（i＝1，2，3）的特征值有且仅有0和1； （2）Ai的对应于特征值1的特征向量是Aj的对应于特征值0的特征向量（i≠j）； （3）若α(→)1、α(→)2、α(→)3分别为A1、A2、A3的对应于特征值1的特征向量，则向量组α(→)1、α(→)2、α(→)3线性无关。正确答案：
(1)设λi为矩阵Ai的特征值,αi(αi≠0)是Ai的属于特征值λi的特征向量,则有λiαi=Aiαi=Ai2αi=λiAiαi=λi2αi,所以(λi-λi2)αi=0。
由αi≠0知λi-λi2=0,所以λi=0或1,即若Ai有特征值,则只能是0或1。
由Ai2=Ai得Ai(Ai-E)=0,因为AiAj=0(i≠j)且Ai≠0(i=1,2,3),所以Ai≠E,即Ai-E≠0。所以知Ai的列向量都是齐次线性方程组AiX=0的解,且AiX=0有非零解。
从而,Ai,=0,即,Ai-0E,=0。即0是Ai的特征值,同理可证1也是Ai的特征值。
(2)设Ai属于特征值1的特征向量为αi,则Aiαi=αi,AjAiαi=Ajαi(i≠j)。
因为AiAj=0(i≠j),所以AjAi=0,Ajαi=0αi,故Ai的属于特征值1的特征向量是Aj属于特征值0的特征向量。
(3)设有数k1,k2,k3使k1α1+k2α2+k3α3=0,即k1A1α1+k2A1α2+k3A1α3=0,根据(2)可知α2,α3应是A1的属于特征值0的特征向量,即A1α2=0,A1α3=0。
故有k1A1α1=k1·1·α1=k1α1=0,由α1≠0,故k1=0。同理可证k2=k3=0,因此α1、α2、α3线性无关。解析： 暂无解析 -
第13题：
设A为n阶实对称矩阵,则().A.A的n个特征向量两两正交
B.A的n个特征向量组成单位正交向量组
C.A的k重特征值λ0,有r(λ0E-A)=n-k
D.A的k重特征值λ。，有r(λ0E-A)=k
参考答案：
-
第14题：
设A是n阶实对称矩阵，则A有n个()特征值.
参考答案：实
-
第15题：
n*n矩阵可看作是n维空间中的线性变换，矩阵的特征向量经过线性变换后，只是乘以某个常数(特征值)，因此，特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1，w2，w3)，其对应的特征值为( )。
A．1／3
B．1
C．3
D．9
正确答案：C
解析：n*n矩阵可看做是n维空间中的线性变换，它将任何一个向量x变换成新的向量(A的矩阵与列向量x的乘积)。三维空间中的旋转变换就是一种线性变换，它将一个变量变换成另一个变量。旋转变换必然绕某个轴旋转，这个轴上的向量经过该旋转变换后得到的向量仍会保持在这根轴上。这根轴上的向量属于该旋转变换的特征向量。对于单纯的旋转变换来说，这根旋转轴上的特征向量所对应的特征值为1。线性变换A的特征向量Y及其相应的特征值λ满足AY=λY，其几何意义是特征向量Y经过线性变换A变换成向量λY(保持在同一轴上，只是乘以常数λ，放大或缩小入倍，λ为负时变为相反方向)。本题中的矩阵A以及由w1、w2、w3组成的列向量w具有关系(可以通过矩阵乘法得到)Aw=3w，所以，(w1、w2、w3)是该矩阵的特征向量，其相应的特征值为3。 -
第16题：
若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为：A. a
B. -a
C. 0
D. a-1答案：A解析：解：本题主要考察两个知识点：特征值的求法及行列的运算。
A的一特征值为a。
选A。 -
第17题：
设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值
B.A是可逆矩阵
C.A存在n个线性无关的特征向量
D.A一定为n阶实对称矩阵答案：C解析：矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C). -
第18题：
已知n阶可逆矩阵A的特征值为λ0，则矩阵(2A)-1的特征值是：
答案：C解析：
-
第19题：
设A,B为n阶矩阵.
(1)是否有AB～BA；(2)若A有特征值1,2,…,n,证明：AB～BA.答案：解析：
-
第20题：
设A为m×n阶实矩阵,且r(A)=n.证明：A^TA的特征值全大于零.答案：解析：
-
第21题：
设2阶矩阵A有两个不同特征值，α1，α2是A的线性无关的特征向量，且满足A^2(α1+α2)=α1+α2，则｜A｜=________.答案：1、-1解析：
-
第22题：
设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。
- A、α是矩阵-2A的属于特征值-2λ的特征向量
- B、α是矩阵的属于特征值的特征向量
- C、α是矩阵A*的属于特征值的特征向量
- D、α是矩阵AT的属于特征值λ的特征向量
正确答案:D -
第23题：
问答题设n阶矩阵A有n个两两正交的特征向量，证明A是对称矩阵。正确答案：
设A的n个两两正交的特征向量为α1,α2,…,αn,其对应的特征值依次为λ1,λ2,…,λn。
令ξi=αi/,αi,(i=1,2,…,n),则ξ1,ξ2,…,ξn是两两正交的单位向量。
记P=(ξ1,ξ2,…,ξn),即P是正交矩阵。从而有P-1=PT,P-1AP=diag(λ1,λ2,…,λn)=Λ,即A=PΛP-1=PΛPT,故AT=(PΛPT)T=(PT)TΛTPT=PΛPT=A,即A是对称矩阵。解析： 暂无解析