考虑背包问题:n=6,物品重量W=(1,5,2,3,6,1),价值P=(15,59,21,30,60,5),背包载重量C=10。能放进背包的物品价值最大为()。A、101B、110C、115D、120
题目
考虑背包问题:n=6,物品重量W=(1,5,2,3,6,1),价值P=(15,59,21,30,60,5),背包载重量C=10。能放进背包的物品价值最大为()。
- A、101
- B、110
- C、115
- D、120
相似考题
更多“考虑背包问题:n=6,物品重量W=(1,5,2,3,6,1),价”相关问题
-
第1题:
阅读下列程序说明和C代码,将应填入(n)处的字句写在对应栏内。
【说明】
“背包问题”的基本描述是:有一个背包,能盛放的物品总重量为S,设有N件物品,其重量分别为w1,w2,…,wn。希望从N件物品中选择若干件物品,所选物品的重量之和恰能放入该背包,即所选物品的重量之和等于S。
如下程序均能求得“背包问题”的一组解,其中程序1是“背包问题”的递归解法,而程序2是“背包问题”的非递归解法。
【程序1】
include<stdio.h>
define N 7
define S 15
int w[N+1]={0,1,4,3,4,5,2,7};
int knap(int s, int n)
{
if(s==0) return 1;
if(s<0 || (s>0 && n<1))return 0;
if((1)){/*考虑物品n被选择的情况*/
printf("%4d",w[n]);
return 1;
}
return (2);/*考虑不选择物品n的情况*/
}
main()
{
if(knap(S,N))printf("OK!\n");
else printf("N0!\n");
}
【程序2】
include<stdio.h>
define N 7
define S 15
typedef struct{
int s;
int n;
int job;
}KNAPTP;
int w[N+1]={0,1,4,3,4,5,2,7};
int knap(int s, int n);
main()
{
if(knap(S,N)) printf("0K!\n");
else printf("N0!\n");
}
int knap(int s, int n)
{
KNAPTP stack[100],x;
int top, k, rep;
x.s=s;x.n=n;
x.job=0;
top=1; stack[top]=x;
k=0;
while( (3) ){
x=stack[top];
rep=1;
while(!k && rep){
if(x.s==0) k=1;/*已求得一组解*/
else if(x.s<0 || x.n<=0) rep=0;
else{
x.s=(4);
x.job=1;
(5)=x;
}
}/*while*/
if(!k){
rep=1;
while(top>=1 && rep){
x=stack[top--];
if(x.job==1){
x.s +=w[x.n+1];
x.job=2;
stack[++top]=x;
(6);
}/*if*/
}/*while*/
}/*if*/
/*while*/
if(k){&nbs
正确答案:(1) knap(s-w[n]n-1) (2) knap(sn-1) (3) top>=1 && !k 或 top>0 && k==0 (4) x.s-w[x.n--] (5) stack[++top] (6) rep=0
(1) knap(s-w[n],n-1) (2) knap(s,n-1) (3) top>=1 && !k 或 top>0 && k==0 (4) x.s-w[x.n--] (5) stack[++top] (6) rep=0 解析:本题考查“背包”问题,这是一个非常经典的问题,一般采用递归法实现。
典型做法是逐个考查每一件物品,对于第i件物品的选择考虑有两种可能。
.考虑物品i被选择,这种可能仅当包含它不会超过方案总重量限制时才是可行的。选中后继续递归考虑其余物品的选择。
.考虑物品i不被选择,这种可能仅当不包含物品i也有可能找到价值更大的方案时才是可行的。
程序1是递归算法实现。对每个物品i,考查选择放入和不放入背包两种情况。函数knap(int s,int n)中,形参s是考查完物品i后背包还能装载的重量,n是考查完物品i后下一个待考查的物品。每次选择一个物品放入背包,那么剩余的物品和背包剩余重量又构成一个“背包问题”。根据注释,空(1)是考查物品n放入背包的情况,既然放入背包,则背包剩余可装重量为 s-w[n],继续考查物品n-1。这点可从主函数的调用形式“knap(S,N)”分析出。故空(1)应填“knap(s-w[n],n-1)”。空(2)是考查物品n不放入背包的情况,既然不放入背包,则背包可装重量仍为s,继续考查物品n-1。故空(2)应填“knap(s,n-1)”。
程序2是非递归算法实现,相对较难。算法思想仍是对每个物品i分别考查选择放入和不放入两种情况,借助栈实现,即数组stack。其实就是手动完成递归算法中由系统自动完成的压栈、出栈操作。
据注释“k=1时则求得一组解”可知k为是否求得解的标志:k=0表示没有解,继续求解。经分析,结构变量KNAPTP表示经过考查的物品:分量s表示考查过该物品后,背包所能盛放的物品的重量,分量n表示待考查的下一个物品在数组w中的下标,分量job表示物品当前的状态,job等于1表示物品n可以放入背包,job等于2表示物品不能放入背包,在以后的选取中将不再考虑该物品,初始时job等于0表示背包中没有放入任何物品。rep是一个标志变量,等于。表示结束当前的动作,等于1表示继续进行当前的动作;当栈顶物品不能装入背包时,将rep置为0,表示下一步不再从数组w中取物品。rep初值为1。x为工作节点。
while( (3) )循环体内的语句可以肯定是考查各个物品n的选择情况。对物品n,先考查将物品放入背包的情况。显然,如果物品n满足放入背包的条件,则空(4)和空(5)完成将物品放入背包的操作,其中空(4)应该是将工作节点x的分量s值减去所考查物品的重量。且n要减1,修改背包可容纳物品的重量和设置下一个待考查物品。而空(5)则需要将修改后的工作节点x送到栈顶,将下一个待考查的物品入栈。故空(4)应填“x.s-w[x.n--]”,空(5)应填“stack[++top]”。
if(!k)后的程序段是处理所考查的物品不满足放入背包的条件时的情况(rep=0,while(!k && rep)循环结束),则将该物品从背包中取出,修改其job值为2,用以标记该物品不能放入背包。修改完后跳出while(top>=1 && rep)循环,因此需要将rep置为0,用以结束循环。故空(6)应填“rep=0”。 -
第2题:
阅读下列说明,回答问题1至问题2,将解答填入答题纸的对应栏内。
【说明】
0—1背包问题可以描述为:有n个物品,对i=l,2,…,n,第i个物品价值为vi,重量为wi(vi和wi为非负数),背包容量为w(W为非负数),选择其中一些物品装入背包,使装入背包物品的总价值最大,即
 ,且总重量不超过背包容量,即
,且总重量不超过背包容量,即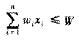 ,其中,xi∈{O,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。
,其中,xi∈{O,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。用回溯法求解此0—1背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点已经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOuND(v,w,k,W)函数,其中v、w、k和w分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。下面给出0—1背包问题的回溯算法伪代码。
函数参数说明如下:w:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
BKNAP(W,n,w,v,fw,fp,X)
1 cw←cp0
2 (1)
3 fp←l
4 while true
5 while k≤n and cw+w[k]≤w d。
6 (2)
7 cp←cp+v[k]
8 Y[k]←l
9 k←k+1
10 if k>n then
11 if fp<cp then
12 fp←cp
13 fw←cw
14 k←n
15 X←Y
16 else Y (k)←O
17 while BOUND(cp,cw,k,W) ≤fp do
18 while k≠O and Y(k)≠l d0
19 (3)
20 if k=0 then return
2l Y[k]←0
22 cw←cw-w[k]
23 cp←cp-v[k]
24 (4)
正确答案:(1)k←1(2)cw←cw+w[k](3)k←k-1(4)k←k+l
(1)k←1(2)cw←cw+w[k](3)k←k-1(4)k←k+l -
第3题:
*部分背包问题可有贪心法求解:计算Pi/Wi
数据结构:
w[i]:第i个背包的重量;
p[i]:第i个背包的价值;
1.0-1背包: 每个背包只能使用一次或有限次(可转化为一次):
A.求最多可放入的重量。
正确答案:NOIP2001 装箱问题
有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若千个装入箱内,使箱子的剩余空间为最小。
l 搜索方法
procedure search(k,v:integer); {搜索第k个物品,剩余空间为v}
var i,j:integer;
begin
if v<best then best:=v;
if v-(s[n]-s[k-1])>=best then exit; {s[n]为前n个物品的重量和}
if k<=n then begin
if v>w[k] then search(k+1,v-w[k]);
search(k+1,v);
end;
end;l DP
F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志,为布尔型。
实现:将最优化问题转化为判定性问题
f [I, j] = f [ i-1, j-w[i] ] (w[I]<=j<=v) 边界:f[0,0]:=true.
For I:=1 to n do
For j:=w[I] to v do F[I,j]:=f[I-1,j-w[I]];
优化:当前状态只与前一阶段状态有关,可降至一维。
F[0]:=true;
For I:=1 to n do begin
F1:=f;
For j:=w[I] to v do
If f[j-w[I]] then f1[j]:=true;
F:=f1;
End; -
第4题:
0-1背包问题可以描述为:有n个物品,对i=1,2,…,n,第i个物品价值为vi ,重量为wi(vi,和wi为非负数),背包容量为W(W为非负数),选择其中一些物品装入背包,使装入背包物品的总价值最大,
 ,且总重量不超过背包容量,即
,且总重量不超过背包容量,即 ,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品 放入背包。
,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品 放入背包。【问题1】(8分)
用回溯法求解此0-1背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点己经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND(v,w,k,W)函数,其中v, w, k和W分别表示当前已经获得的价值、当前背包的重量、己经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。
下面给出0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
BKNAP(W,n,w,v,fw,fp,X)
1 cw ← cp ← 0
2 (1)
3 fp ← -1
4 while true
5 while k≤n and cw+w[k]≤W do
6 (2)
7 cp ← cp+v[k]
8 Y[k]← 1
9 k ← k+1
10 if k>n then
11 if fp<cp then
12 fp ← cp
13 fw ← ew
14 k ← n
15 X ← Y
16 else Y(k)← 0
17 while BOUND(cp,cw,k,W) ≤fp do
18 while k≠0 and Y(k)≠1 do
19 (3)
20 if k=0 then return
21 Y[k]←0
22 cw ← cw ← w[k]
23 cp ← cp ← v[k]
24 (4)
正确答案:本题考查的是用回溯法求解0-1背包问题。回溯法有两类算法框架:非递归形式和递归形式,本题采用非递归形式表示。理解回溯法的基本思想和这两类算法框架是正确解答本题的根本要求·回溯法从第一项物品开始考虑是否应该装入背包中,因此当前考虑的物品编号k从1开始,即k←1。然后逐项往后检查,若能全部放入背包则将该项放入背包,此时背包的重量应该是当前的重量加上当前考虑物品的重量,即cw←cw+w[k],当然背包中物品的价值也为当前的价值加上当前考虑物品的价值。若己经考虑完了所有的物品,则得到一个解,判断该解是否为当前最优,若为最优,则将该解的信息放入变量fp、fw和X中。若还没有考虑完所有的物品,意味着有些物品不能放入背包,此时先判断若不将当前的物品放入背包中,则其余物品放入背包是否可能得到比当前最优解更优的解,若得不到则回溯;否则继续考虑其余的物品。
【问题1】(共8分,各2分)
(1)k ← 1 或其等价形式
(2)cw ← cw + w[k] 或其等价形式
(3)k ← k – 1 或其等价形式
(4)k ← k + l 或其等价形式
-
第5题:
考虑一个背包问题,共有n=5个物品,背包容量为W=10,物品的重量和价值分别为:w={2,2,6,5,4},v={6,3,5,4,6},求背包问题的最大装包价值。若此为0-1背包问题,分析该问题具有最优子结构,定义递归式为

其中c(i,j)表示i个物品、容量为j的0-1背包问题的最大装包价值,最终要求解c(n,W)。 采用自底向上的动态规划方法求解,得到最大装包价值为(62),算法的时间复杂度为(63)。 若此为部分背包问题,首先采用归并排序算法,根据物品的单位重量价值从大到小排序,然后依次将物品放入背包直至所有物品放入背包中或者背包再无容量,则得到的最大装包价值为(64),算法的时间复杂度为(65)。
A.11
B.14
C.15
D.16.67
正确答案:C
-
第6题:
考虑下述背包问题的实例。有5件物品,背包容量为100,每件物品的价值和重量如下表所示,并已经按照物品的单位重量价值从大到小徘好序,根据物品单位重量价值大优先的策略装入背包中,则采用了(请作答此空)设计策略。考虑0/1背包问题(每件物品或者全部放入或者全部不装入背包)和部分背包问题(物品可以部分装入背包),求解该实例,得到的最大价值分别为( )。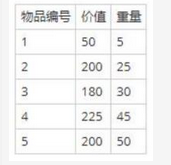 A.分治
A.分治
B.贪心
C.动态规划
D.回溯答案:B解析:贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。0/1背包考虑该问题时,只能放入1、2、3号物品,故总价值为430,采用部分背包问题可以将物品拆分,故放1、2、3号物品后还可以放入部分4号物品,故总容量为630。 -
第7题:
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。【说明】0-1背包问题定义为:给定1个物品的价值v[1....i]、重量w[1....i]和背包容量T,每个物品装到背包里或者不装到背包里,求最优的装包方案,使得所得到的价值最大。0-1背创问题具有最优子结构性质,定义c为最优装包方案所获得的最大价值则可得到如下所示的递归式。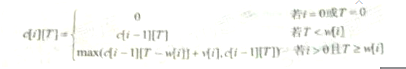
【C代码】下面是算法的C语言实现(1)常量和变量说明T:背包容量V[]:价值数组W[]:重量数组C[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值(2)C程序

【问题1】(8分)根据说明和C代码,填充C代码中的空(1)~(4)【问题2】(4分)根据说明和C代码,算法采用了(5)设计策略。在求解过程中,采用了(6)(自底向上或者自顶向下)的方式。【问题3】(3分)若5项物品的价值数组和重量数组分别为v[]={0,1,6,18,22,28}和w[]={0,1,2,5,6,7},背包容量为T=11,则获得的最大价值为(7)。答案:解析:问题1:1:c[i][j]2: temp第8题:
对于如下描述的背包问题,请计算最终装入背包的最大价值和以及各个物品装入背包的数量。 背包容量:C=50千克。3件物品。物品1重20千克,价值100元;物品2重20千克,价值120元;物品3重30千克,价值90元。
正确答案: 物品1的单位重量价值为50元/千克;物品2的单位重量价值为60元/千克;物品3的单位重量价值为30元/千克。采用贪心算法解此背包问题。
此时,贪心的策略是:每次选择单位重量价值最大的物品。因此,首先选择物品2,然后是物品1,最后是物品3,直至将背包装满。
物品2全部装入背包,当前背包中价值120元,背包占用20千克,剩余30千克;
物品1全部装入背包,当前背包中价值220元(120元+100元),背包占用40千克,剩余10千克;
物品3的1/3被装入背包,当前背包中价值250元(120元+100元+90元×1/3),背包占用50千克(装满)。
因此,最终装入背包的最大价值为250元,物品1和物品2都全部装入,分别是20千克和20千克,物品3装入1/3,是10千克。第9题:
在0-1背包问题中,若各物品依重量递增序排列时,其价值恰好依递减序排列,对这个特殊的0-1背包问题,设计一个有效的算法找出最优解。(描述你的算法即可,无需证明算法的正确性)
正确答案: 对于0-1背包问题本来是无法用贪心算法得到最优解的,但对于这类特殊的0-1背包问题,则可以用贪心算法去解。贪心策略如下:
首先将各物品依重量递增序(即也是价值递减序)排列,然后依照价值递减顺序选择物品装入背包,直到背包装不下下一件物品为止。
这里贪心算法的贪心选择策略是:每次总是选择价值最大(同时重量也最小)的物品,然后检查是否可以装入背包。第10题:
举反例证明0/1背包问题若使用的算法是按照pi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明0/1背包问题与背包问题的不同)。
正确答案: 举例如:
p{7,4,4},w={3,2,2},c=4时,
由于7/3最大,
若按题目要求的方法,只能取第一个,收益是7。
而此实例的最大的收益应该是8,取第2,3 个。第11题:
单选题()是油脂酸价测定的计算公式。A酸价(mgKOH/g油)=V×N×56.1/W×100
B酸价(mgKOH/g油)=W×100/V×N×56.1
C酸价(mgKOH/g油)=V×N/W×100
正确答案: C解析: 暂无解析第12题:
问答题有这样一类特殊0-1背包问题:可选物品重量越轻的物品价值越高。 n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大,能获得的最大总价值多少?正确答案: 因为该0-1背包问题比较特殊,恰好重量越轻的物品价值越高,所以优先取重量轻的物品放进背包。最终可以把重量分别为2,3,4,5的三个物品放进背包,得到的价值和为15+8+6+4=33,为最大值。解析: 暂无解析第13题:
阅读下列函数说明和C代码,填入(n)处字句,并回答相应问题。
[说明]
背包问题就是有不同价值、不同重量的物品n件,求从这n件物品中选取一部分物品的选择方案,使选中物品的总重量不超过指定的限制重量,而且选中物品的价值之和为最大。
背包问题是一个典型的NP完全难题。对该问题求解方法的研究无论是在理论上,还是在实践中都具有一定的意义。如管理中的资源分配、投资决策、装载问题等均可建模为背包问题。
常用的背包问题求解方法很多,但本题中采用了一种新的算法来求解背包问题。该算法思想为:首先要对物品进行价重比排序,然后按价重比从大到小依次装进包裹。这种方法并不能找到最佳的方案,因为有某些特殊情况存在,但只要把包中重量最大的物品取出,继续装入,直到达到limitweight,这时的物品就是limit weight的最大价值。这种算法不需要逐个进行试探,所以在数据非常大时,执行效率主要由排序的时间复杂度决定。该算法的流程图为图11-4。
仔细阅读程序说明和C程序流程图及源码,回答问题1和问题2。
[流程图11-4]
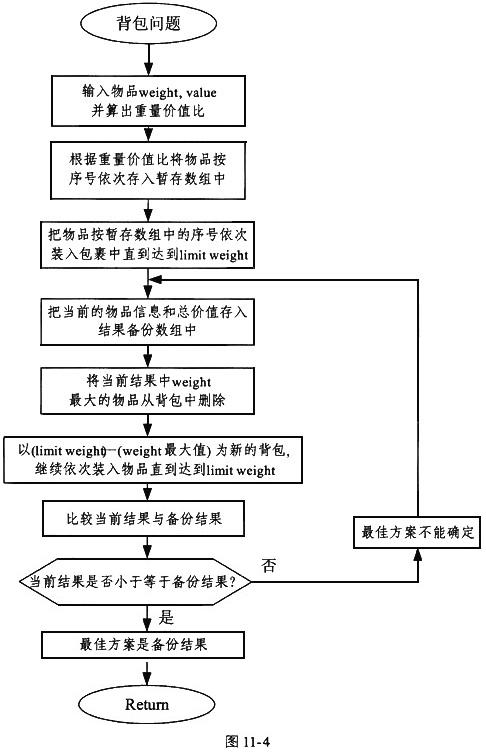
[程序说明]
struct Thing:物品结构
typedef struct Bag:背包结构类型
input ( ):将物品按序号依次存入数组函数
inbag ( ):物品按物价比入包函数
init ( ):初始化函数
sort ( ):对物品按价格重量比排序函数
outbag ( ):取出包中weiht最大的物品函数
print ( ):最佳方案输出函数
[C程序]
define N 255
struct Thing {
double weight;
double value;
double dens;
}thing[N];
typedef stmct Bag {
Thing thing [N];
double weighttmp;
double sumvalue;
}bag,best;
inbag ( )
{
do{
bag.thing[i]=thing[i]
(1)
(2)
i++;
}while ( (3) )
}
init ( )
{
for (inti=0; i<N; i++)
{
input (thing[i].weight, thing [i].value)
thing [i].dens=thing[i].value/thing [i].weight;
};
}
main ( )
{
init ( );
sort ( );
inbag ( );
do {
best=bag; //把包中物品放入暂存数组
outbag ( ); //取出包中weight最大的物品
(4)
}while ( (5))
print (best); //输出temp因为是最佳方案
}
根据程序说明及流程图、部分C源码,充分理解算法思想,填入(n)处。
正确答案:(1)bag.weighttmp=bag.weighttmp+thing[i].weight; (2)bag.sumvalue=bag.sumvalue+thing[i].value; (3)bag.weighttmp=weightlimit (4)inbag( ); (5)best.sumvaluebag.sumvalue
(1)bag.weighttmp=bag.weighttmp+thing[i].weight; (2)bag.sumvalue=bag.sumvalue+thing[i].value; (3)bag.weighttmp=weightlimit (4)inbag( ); (5)best.sumvaluebag.sumvalue第14题:
阅读以下程序说明和C程序,将程序段中(1)~(7)空缺处的语句填写完整。
【说明】
【C程序1】用回溯算法来产生由0或1组成的2m个二进位串,使该串满足以下要求。
视串为首尾相连的环,则由m位二进制数字组成的2m个子序列,每个可能的子序列都互不相同。例如,如果m=3,在串11101000首尾相连构成的环中,由3位二进制数字组成的每个可能的子序列都在环中恰好出现一次,它们依次是111,110,101,010,100,000,001,011,如图2-14所示。
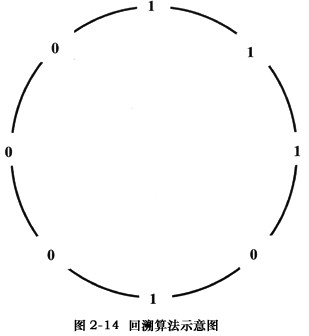
【C程序2】是求“背包问题”的一组解的递归算法程序。“背包问题”的基本描述是:有一个背包,能盛放的物品总重量为S,设有N件物品,其重量分别为W1,W2,…,Wn,希望从N件物品中选择若干件物品,所选物品的重量之和恰能放入该背包,即所选物品的重量之和等于S。
【C程序1】
define N 1024
define M 10
int b [N+M-1]
int equal(int k, int j int m) {
int i;
for(i=0; i<m; i++
if ( b[ k + i] (1) )
return 0;
return 1; }
int exchange (int k, int m, int v){
while ( b[ k + m - 1 ) == v ) {
b[ kncm--i]=! v (2);
}
(3)=v;
return k;
}
init ( iht v) {
int k
for( k = 0;K = N + M - 1;k++)
b[k] = v;
}
main ( ) {
int m, v, k, n, j;
printf ('Enter m (l<m<10) , v v=0, v=1)\ n") ;
scanf (" %d%d , &m, &v);
n = 0x01 << m;
init (!v);
k=0;
while((4)< n)
for (j=0;j<k;j++)
if (equal (k, j, m)) {
k=exchange (k, m, v)
j=(5);
}
for (k= 0 ;k<n ;k++ )
print{ (" %d\ n" , b[k]) ;
}
}
【C程序2】
include<stdio. h>
define N 7
define S 15
int w[N+1] = {0, 1, 4, 3, 4, 5, 2, 7};
int knap (int S, int n){
if (S == 0)
return 1;
if (s<0 || (s>0 && n<1))
return 0;
if ((6))) {
printf( "4d", w[n]);
return 1;
}
return (7)
}
main ( ) {
if (knap (S, N)
printf("OK:\n");
else
printf("NO!\n")
}
正确答案:(1)!=b[j+1] (2)k-或-k或k=k-1或k-=l或其他等价形式 (3)b[k+m-1] (4)++k或(k=k+1)或(k+=1)或其他等价形式 (5)-1 (6)knap(s-w[n]n-1) (7)knap(sn1)
(1)!=b[j+1] (2)k-,或-k,或k=k-1,或k-=l,或其他等价形式 (3)b[k+m-1] (4)++k,或(k=k+1),或(k+=1),或其他等价形式 (5)-1 (6)knap(s-w[n],n-1) (7)knap(s,n,1) 解析:这是一道要求读者掌握回溯算法和递归算法的C语言编程题。解答此类题目的一般思路是读懂程序说明部分,弄清楚程序中各变量及各函数的含义,认真分析程序。本试题的解答思路如下。
回溯算法也称为试探算法。该方法首先暂时放弃关于问题规模大小的限制,并将问题的候选解按某种顺序逐一枚举和检验。当发现当前候选解不可能是解时,就选择下一个候选解;倘若当前候选解除了不满足问题规模要求外,还不满足所有其他要求时,继续扩大当前候选解的规模,并继续试探。如果当前候选解满足包括问题规模在内的所有要求时,该候选解就是问题的一个解。在回溯算法中,放弃当前候选解寻找下一个候选解的过程称为回溯,扩大当前候选解的规模并继续试探的过程称为向前试探。
用回溯算法可以求得问题的一个解或全部解。为了不重复搜索已经试探过的解,需要采取某种方法来标记,最常用的方法是用栈(数组)来记录已经找到的解或搜索过的情况(路径),也可以用位置指针、值的排列顺序等来标记。回溯算法的重点与难点如下。
1)用回溯算法求问题的一个解时,找到的解不一定是最优解。在编写这类程序时,要注意记录(或标记)好中间每一个项的值,以便回溯。回溯到起始处,表示无解。
2)用回溯算法求问题的全部解时,要注意在找到一组解时应及时输出或记录下来并统计解的个数,马上改变当前项的值并继续寻找下一组解,防止找到的解重复。回溯到起始位置表示找到了问题的全部解(尽管可能一组解也没输出)。
认真阅读题干的程序说明和所给出的C程序段可知,【C程序1】由4个函数组成。①主函数main()的功能是初始化,在循环语句中调用函数依次产生二进位串,之后输出产生的二进位串;②函数init()对二进位串数组b进行初始化置位,全部置0或置1;③函数int equal()判断数组b中是否保存有相同的子串;④函数int exchange()将数组b中新加入的从k开始的子串最后一位由0变1或由1变0。
(1)空缺处在函数int equal()中判断二进制串数组b中是否存在与新加入的子串相等的子串。新加入的子串在b中的开始下标为k,程序将b数组中k开始的m个字符逐个和i开始的m个字符相比较,又因为在主函数中有语句if(equal(k,j,m))(k=exchange(k,m,v);……),说明若m个字符都相等,则返回1,执行语句“k=exchange(k,m,v);”来修改新加入的子串,否则只要有一个字符不等,则返回0。所以(1)空缺处所填写的内容是“!=b[j+i]”。
(2)、(3)空缺处在函数int exchange()中的作用是修改新加入的子串,即将新子串的最后一个字符由 0变1或由1变0。如果修改后,经测试仍有相同的子串存在,则要回溯到b中的前一个子串,然后修改这个子串的最后一个字符,重复上述过程。当循环条件成立时新子串最后一个brk+m-1]修改后仍存在相同的子串,则要求回溯。而k为新子串在b数组中的开始下标,所以(2)空缺处所填写的内容是“k=k-1 (或其他等价形式,如--k,或k--,或k-=1)”。
(3)空缺处所在的语句是处理不需要回溯的情况,此时要将新子串最后一个b(k+m-1]修改,又因为b[k+m-1]初值为!v,所以修改后的b[k+m-1]值应为v,所以(3)空缺处所填写的内容是“b(k+m-1]”。
(4)、(5)空缺处在主程序main()中。依次往b数组中加入新子串,加入方式是对b数组都考查一个字符,即当加入子串在b数组中的下标k加1后,k又变成下两个新加入子串的下标。所以k+1也是在b数组中正确填写的二进制数的个数,根据题意其值不超过n。所以(4)空缺处所填写的内容是“k=k+1(或其他等价形式,如++k,或k+=1)”。
根据(5)空缺处的前后语句可知,若函数equal返回1,即两个二进制字串相等,表示此步试探失败,此时调用函数exchange对新加入子串的最后一个字符进行修改或回溯,并返回修改或回溯后的最后一个子串在b数组中的下标k值。更改后,又要从第一个m位二进制字串开始检查,即要让for循环重新开始,此时j应为0。因为for循环语句每执行一次,要执行j++,所以(5)空缺处所填写的内容是“-1”。
递归是设计和描述算法的一种有力的工具。能采用递归描述的算法通常有这样的特征:为求解规模为 N的问题,设法将它分解成一些规模较小的问题,然后由这些小问题的解方便地构造出大问题的解,并且这些规模较小的问题也能采用同样的分解和综合方法,分解成规模更小的问题,并由这些更小问题的解构造出规模稍大问题的解。特别地,当规模N=1时,能直接得到解。递归算法重点与难点如下 。
1)编写递归程序的关键是:找出问题的递归关系和初始值。可以利用归纳法由一个问题归纳总结出递归式,加上初始条件,即可编写递归函数。
2)编写递归程序时,必须要给出递归结束条件。
3)递归的次数不是无限制的,每一次的递归调用都要压栈,占用内存,而计算机的内存是有限的。
4)采用递归方法定义的数据结构或问题最适合使用递归方法。
【C程序2】用递归算法解决背包问题的思路是对于物品i的选择有两种可能。
1)考虑物品i被选择的情况,这种可能性当且仅当包含它不会超过方案总重量的限制时才是可行的。物品i被选择后,继续递归去考虑下一个物品。
2)考虑物品i不被选择的情况,这种可能性当且仅当不包含物品i时,或找到价值更大的方案。考虑完物品i后,也要继续递归考虑下一个物品。
根据以上思路分析【C程序2】中的函数knap(int s,intn)是用递归算法解决“背包问题”的。其中,参数s为考查完物品i后,背包还能盛放的重量:n为考查完物品i后,下一个待考查的物品。(6)空缺处是考虑物品n被选择的情况,此时因为物品n已被选择,所以剩余可盛放的重量应为s-w[n],而背包待考查物品应为n-1,则(6)空缺处所填写的内容是“knap(s-w[n]n-1)”。
(7)空缺处是处理不包含物品i时的情况。由于物品i没有放入背包,则背包可装载重量不变还应是 s,而这时应该考虑下一个物品n-1。因此(7)空缺处所填写的内容是“knap(s,n-1)”。第15题:
利用贪心法求解0/1背包问题时,(55)能够确保获得最优解。用动态规划方法求解 0/1背包问题时,将“用前i个物品来装容量是X的背包”的0/1背包问题记为KNAP(1,i,X),设fi(x)是KNAP(1,i,X)最优解的效益值,第j个物品的重量和放入背包后取得效益值分别为 wj和pj(j=1~n)。则依次求解f0(x)、f1(x)、...、fn(X)的过程中使用的递推关系式为(56)。.
A.优先选取重量最小的物品
B.优先选取效益最大的物品
C.优先选取单位重量效益最大的物品
D.没有任何准则
正确答案:D
解析:本题考查0/1背包问题的动态规划求解方法。
利用贪心法可以解决普通背包问题(即允许将物品的一部分装入背包),此时使用“优先选取单位重量效益最大的物品”的量度标准可以获得问题最优解,但是贪心法不能用来求解0/1背包问题,题目中供选择的A、B、C三种量度标准均不能确保获得最优解。
利用动态规划求解0/1背包问题时,按照题目中约定的记号。KNAP(1,i,X)的最优解来自且仅来自于以下两种情况之一:
. 第i个物品不装入背包,此时最优解的值就是子问题KNAP(1,i-1,X)的最优解的效益值,即为fi-1(X);
. 第i个物品装入背包,此时最优解的值为第i个物品的效益值与子问题 KNAP(1,i-1,X-wi)的最优解效益值之和,即为fi-1(X-wi)+pi。
综上,KNAP(1,i,X)最优解的值为以上两种情况中效益值更大者,即取max。第16题:
利用贪心法求解0/1背包问题时,(26)能够确保获得最优解。用动态规划方求解O/1背包问题时,将“用前i个物品来装容量是x的背包”的0/1背包问题记为KNAP(1,i,X)设fi(X)是KNAP(1,i,X)最优解的效益值,第j个物品的重量和放入背包后取得效益值分别为W和p(j=1~n),则依次求解f0(X),f1(X),…,fn(X)的过程中使用的递推关系式为(27)。
A.优先选取重量最小的物品
B.优先选取效益最大的物品
C.优先选取单位重量效益最大的物品
D.没有任何准则
正确答案:C
第17题:
【问题 1】(8 分)
用回溯法求解此 0-1 背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点已经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND( v,w,k,W )函数,其中 v、w、k 和 W分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。
下面给出 0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
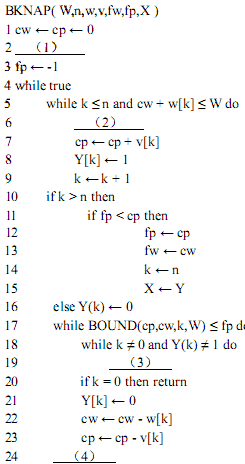 正确答案:
正确答案:
(1)k←1或其等价形式(2)cw←cw+w[k]或其等价形式(3)k←k–1或其等价形式(4)k←k+l或其等价形式第18题:
考虑下述背包问题的实例。有5件物品,背包容量为100,每件物品的价值和重量如下表所示,并已经按照物品的单位重量价值从大到小徘好序,根据物品单位重量价值大优先的策略装入背包中,则采用了( )设计策略。考虑0/1背包问题(每件物品或者全部放入或者全部不装入背包)和部分背包问题(物品可以部分装入背包),求解该实例,得到的最大价值分别为(请作答此空)。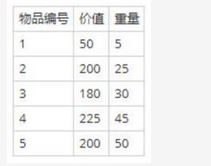 A.605和630
A.605和630
B.605和605
C.430和630
D.630和430答案:C解析:贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。0/1背包考虑该问题时,只能放入1、2、3号物品,故总价值为430,采用部分背包问题可以将物品拆分,故放1、2、3号物品后还可以放入部分4号物品,故总容量为630。第19题:
有0-1背包问题如下: n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大。 P=(15,8,6,4,3,1),W=(2,3,4,5,8,10),单位重量物品价值(7.5,2.67,1.5,0.8,0.375,0.1)
正确答案: 可知随着物品的重量增加,物品的价值减少;因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
1.先把重量为2的物品放进背包,此时剩余载重量为17,P为15。
2.把重量为3的物品放进背包,此时剩余载重量为14,P为23;
3.把重量为4的物品放进背包,此时剩余载重量为10,P为29;
4.把重量为5的物品放进背包,此时剩余载重量为5,P为33;
由于8>5,所以不能再放进背包。
结果是把重量为2,3,4,5的物品装进背包,总价值最大为33。第20题:
有这样一类特殊0-1背包问题:可选物品重量越轻的物品价值越高。 n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大,能获得的最大总价值多少?
正确答案: 因为该0-1背包问题比较特殊,恰好重量越轻的物品价值越高,所以优先取重量轻的物品放进背包。最终可以把重量分别为2,3,4,5的三个物品放进背包,得到的价值和为15+8+6+4=33,为最大值。第21题:
关于背包加密算法的描述中,正确的是()
- A、保证绝对安全
- B、物品总重量公开
- C、背包问题属于NP问题
- D、属于对称加密算法
- E、一次背包已不安全
正确答案:B,C,E第22题:
问答题举反例证明0/1背包问题若使用的算法是按照pi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明0/1背包问题与背包问题的不同)。正确答案: 举例如:
p{7,4,4},w={3,2,2},c=4时,
由于7/3最大,
若按题目要求的方法,只能取第一个,收益是7。
而此实例的最大的收益应该是8,取第2,3 个。解析: 暂无解析第23题:
问答题有0-1背包问题如下: n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大。 P=(15,8,6,4,3,1),W=(2,3,4,5,8,10),单位重量物品价值(7.5,2.67,1.5,0.8,0.375,0.1)正确答案: 可知随着物品的重量增加,物品的价值减少;因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
1.先把重量为2的物品放进背包,此时剩余载重量为17,P为15。
2.把重量为3的物品放进背包,此时剩余载重量为14,P为23;
3.把重量为4的物品放进背包,此时剩余载重量为10,P为29;
4.把重量为5的物品放进背包,此时剩余载重量为5,P为33;
由于8>5,所以不能再放进背包。
结果是把重量为2,3,4,5的物品装进背包,总价值最大为33。解析: 暂无解析
