设Y~,A=,求矩阵A可对角化的概率.
题目
设Y~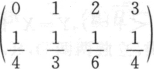 ,A=
,A=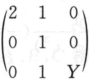 ,求矩阵A可对角化的概率.
,求矩阵A可对角化的概率.
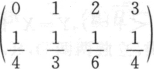 ,A=
,A=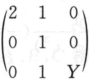 ,求矩阵A可对角化的概率.
,求矩阵A可对角化的概率.相似考题
更多“设Y~,A=,求矩阵A可对角化的概率.”相关问题
-
第1题:
设随机变量(X,Y)的联合密度函数为f(x,y)=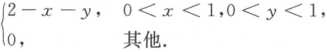 (1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析:
(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析: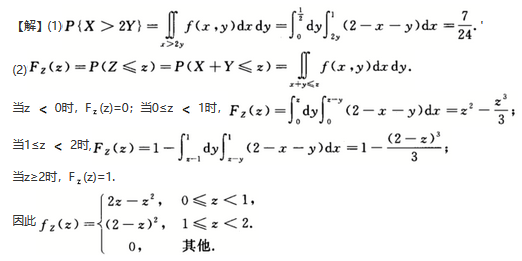
-
第2题:
设随机变量X的概率密度为fx(x)=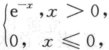 求y=e^x的概率密度FY(y).答案:解析:
求y=e^x的概率密度FY(y).答案:解析: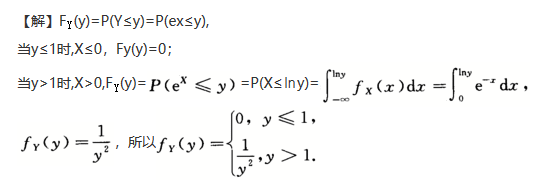
-
第3题:
设X,y的概率分布为X~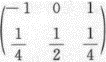 ,Y~
,Y~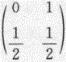 ,且P(XY=0)=1.
,且P(XY=0)=1.
(1)求(X,Y)的联合分布;(2)X,Y是否独立?答案:解析:
-
第4题:
设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2,与y=0所围成的三角形区域.
(Ⅰ)求X的概率密度fx(x);
(Ⅱ)求条件概率密度.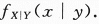 答案:解析:
答案:解析:
-
第5题:
设n阶矩阵A 满足 ,其中s≠t,证明A可对角化答案:解析:
,其中s≠t,证明A可对角化答案:解析:
-
第6题:
设(X,Y)的联合概率密度为f(x,y)=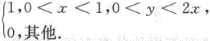 求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.答案:解析:
求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.答案:解析:
-
第7题:
设A=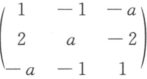 ,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.答案:解析:
,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.答案:解析:
-
第8题:
设二维离散型随机变量(X,Y)的概率分布为
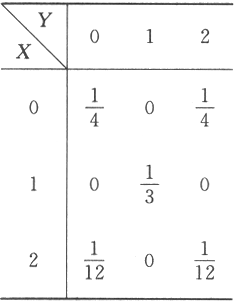
(Ⅰ)求P{X=2Y);
(Ⅱ)求Cov(X-Y,Y).答案:解析:
-
第9题:
设随机变量X与Y的概率分布分别为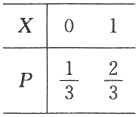 ,
,
且P{X^2=Y^2}=1.
(Ⅰ)求二维随机变量(X,Y)的概率分布;
(Ⅱ)求Z=XY的概率分布;
(Ⅲ)求X与Y的相关系数ρXY.答案:解析:
-
第10题:
设随机变量X的概率密度为
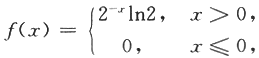
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数.
(Ⅰ)求Y的概率分布;
(Ⅱ)求EY.答案:解析:【分析】令A={对X进行一次观测得到的值大于3}.
【评注】本题类似于我们在2000年出的几何分布考题.从建模到用幂级数在其收敛区间内可逐项求导求和会有不少考生感到困难,本题要比2000年的难一些. -
第11题:
设随机变量X,Y相互独立,且X的概率分布为P{X=0)=P{X=2)= ,Y的概率密度为
,Y的概率密度为
(Ⅰ)求P{Y≤EY};
(Ⅱ)求Z=X+Y的概率密度.答案:解析:
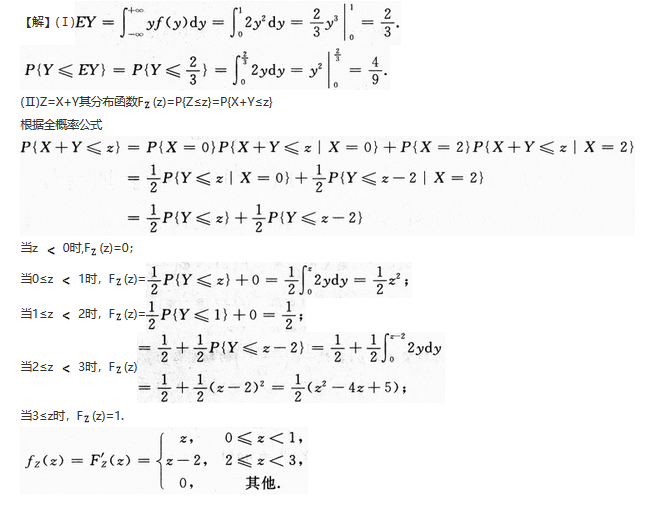
-
第12题:
问答题设X与Y相互独立,X的概率密度为 Y的概率密度为 求:(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y),ρXY.正确答案:解析: -
第13题:
设n阶矩阵A满足(aE-A)(bE-A)=O且a≠6.证明:A可对角化.答案:解析:【证明】由(aE-A)(bE-A)=O,得|aE-A|·|bE-A|=0,则|aE-A|=0或者
|bE-A|=0.又由(aE-A)(bE-A)=O,得r(aE-A)+r(bE-A)≤n.
同时r(aE-A)+r(bE-A)≥r[(aE-A)-(bE-A)]=r[(a-b)E]=n,
所以r(aE-A)+r(bE-A)=n.
(1)若|aE-A|≠0,则r(aE-A=n,所以r(bE-A)=0,故A=bE.
(2)若|bE-A|≠0,则r(bE-A)=n,所以r(aE-A)=0,故A=aE.
(3)若|aE-A|=0且|bE-A|=0,则a,b都是矩阵A的特征值.
方程组(aE-A)X=0的基础解系含有n-r(aE-A)个线性无关的解向量,即特征值a对应的线性无关的特征向量个数为n-r(aE-A)个;
方程组(bE-A)X=0的基础解系含有n-r(bE-A)个线性无关的解向量,即特征值b对应的线性无关的特征向量个数为n-r(bE-A)个.
因为n-r(aE-A)+n-r(bE-A)=n,所以矩阵A有n个线性无关的特征向量,所以A一定可以对角化. -
第14题:
设Α是正定矩阵,B是实对称矩阵,证明ΑB可对角化答案:解析:
-
第15题:
设3阶矩阵A 满足 ,证明A可对角化答案:解析:
,证明A可对角化答案:解析:
-
第16题:
设随机变量X与Y独立,其中X的概率分布为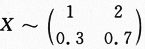 而Y的概率密度为f(y),求随机变量U=X+Y的概率密度g(u).答案:解析:【简解】本题是2003年数三的考题,考查一个离散型和一个连续型两个随机变量的函数的分布,随机变量的独立性等,
而Y的概率密度为f(y),求随机变量U=X+Y的概率密度g(u).答案:解析:【简解】本题是2003年数三的考题,考查一个离散型和一个连续型两个随机变量的函数的分布,随机变量的独立性等,
先求分布函数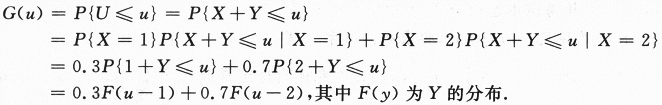
由此得g(u)=0.3f(u-1)+0.7f(u-2). -
第17题:
设矩阵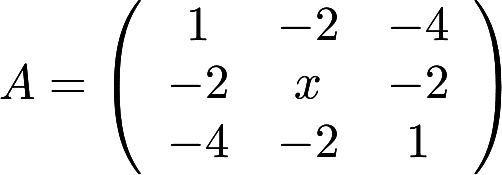 与
与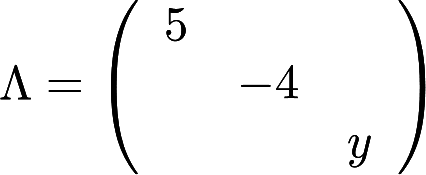 相似,求x, y,并求一个正交阵P,使
相似,求x, y,并求一个正交阵P,使 。答案:解析:
。答案:解析:
-
第18题:
判断矩阵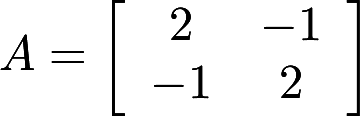 是否可对角化?若可对角化,求可逆矩阵使之对角化。答案:解析:
是否可对角化?若可对角化,求可逆矩阵使之对角化。答案:解析:
-
第19题:
设矩阵A=
(1)已知A的一个特征值为3,试求y;
(2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.答案:解析:
-
第20题:
设二维随机变量(X,Y)的概率密度为
求常数A及条件概率密度. 答案:解析:
答案:解析:

-
第21题:
设随机变量X的概率密度为 令随机变量
令随机变量 ,
,
(Ⅰ)求Y的分布函数;
(Ⅱ)求概率P{X≤Y}.答案:解析:【分析】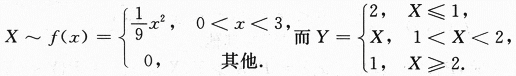
Y是随机变量X的函数,只是这函数是分段表示的,这样得到的Y可能是非连续型,也非离散型,
【解】(Ⅰ)设Y的分布函数为FYy),显然P{1≤Y≤2}=1,所以,
当y<1时,FY(y)=P{Y≤y)=0;
当1≤y<2时,FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1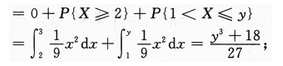
当2≤y时,FY(y)=P{Y≤y}=P{Y≤2}=1.
总之,Y的分布函数为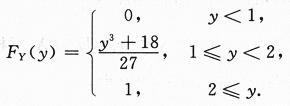
(Ⅱ)因为Y=

-
第22题:
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=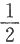 ,Y服从参数为λ的泊松分布.令Z=XY.
,Y服从参数为λ的泊松分布.令Z=XY.
(Ⅰ)求Cov(X,Z);
(Ⅱ)求Z的概率分布.答案:解析:
-
第23题:
问答题设随机变量(X,Y)的概率密度为 求:(1)系数k. (2)边缘概率密度fX(x),fY(y). (3)P{X+Y>1}.正确答案:解析:
